Wskaźniki – nowy cykl edukacyjny

Tzw. „przeciętnemu Kowalskiemu” niekiedy ciężko wyciągnąć prawidłowe wnioski z analizy wszystkich parmetrów i wskaźników dotyczących instrumentów finansowych. Spieszymy z pomocą i rozpoczynamy nowy cykl opisujący najpopularniejsze miary dotyczące funduszy. Na pierwszy ogień idzie zmienność.

Ryzyko zmienności jest nieodłącznym elementem inwestycji. Jednak co istotne, jest to jeden z tych parametrów, na które inwestor może mieć pewien wpływ. W przypadku stopy zwrotu można tylko patrzeć i trzymać kciuki – natomiast poziom ryzyka można kontrolować. Dzieje się to np. poprzez ograniczenie bardziej ryzykownych funduszy/klas aktywów w portfelu lub ustalenia maksymalnej straty (tzw. stop-loss). Jednakże aby właściwie ocenić ryzyko inwestycji, najpierw należy je zmierzyć i porównać z innymi opcjami. W tym celu można wykorzystać różne miary, z których dwie najpopularniejsze przedstawiamy poniżej.

Odchylenie standardowe
To bardzo popularna miara, a do tego relatywnie łatwa do obliczenia i interpretacji. Najpierw formalność, a dla wielu czytelników powtórka ze statystyki – czyli wzór obliczeniowy: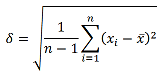


gdzie,
n-liczebność próby, x_i-obserwacja dla x w zadanym momencie, x̄ - przeciętna wartość x.
Wzór wygląda wręcz odpychająco, ale w praktyce nie jest tak źle. Formuła polega na zsumowaniu kwadratów odchyleń od średniej, podzieleniu tej sumy przez liczebność próby (pomniejszoną o 1) i wyciągnięcia pierwiastka z ostatecznej liczby. Wygląda na złożony proces, ale poniższa tabela ilustruje proces krok po kroku: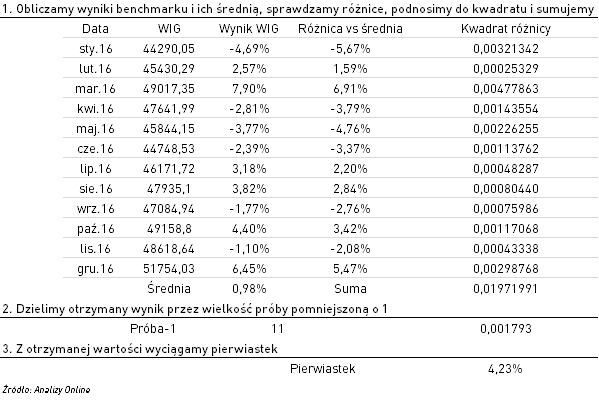


Do problemu można podejść jeszcze prościej – wykorzystać arkusz kalkulacyjny i dostępne funkcje. W przypadku MS Excel funkcja [ODCH.STANDARD.PRÓBKI] zwraca taki sam wynik, jak otrzymany w tabeli. Warto pamiętać o niuansie, jakim jest (n-1) we wzorze.

(sprawdź wyniki funduszy akcji polskich uniwersalnych)

Przyjmijmy upraszczające, ale konieczne założenie, że stopy zwrotu mają rozkład normalny. Jak interpretować otrzymany wynik, u nas 4,23%? Otóż o tyle przeciętnie mogą odchylać się wyniki od średniej z obserwacji. Innymi słowy, jeżeli przeciętny miesięczny wynik dla WIG-u wyniósł ok. 1%, to każdy oddalony o 4,23% od tej wartości nie będzie niczym niezwykłym. Można to skwantyfikować jeszcze lepiej – z teorii statystyki wynika, że wyniki w obszarze (czyli u nas <-3,25%,5,21%>) stanowią 68,2% wszystkich obserwacji. Jeżeli poszerzymy przedział o kolejne odchylenie (odejmując/dodając), obejmiemy 95,4% obserwacji. W rezultacie odchylenie standardowe daje nam obraz, jakich wyników możemy oczekiwać, a jakie są mało prawdopodobne. Trzeba jednak pamiętać, że odchylenie standardowe to wielkość nominalna, którą trudno intepretować „w próżni” – potrzebny jest punkt odniesienia. Inaczej ocenia się liczbę typu 4,23% w izolacji, inaczej zaś gdy wiemy, że np. rozważany do zakupu fundusz charakteryzuje się odchyleniem typu 6%. Zmienność tegoż funduszu jest wyższa od WIG-u, zatem potencjalnie charakteryzuje się on większym ryzykiem, co nie każdemu musi odpowiadać.

Tracking Error
W istocie rzeczy tracking error (pol. błąd odwzorowania) to szczególny rodzaj odchylenia standardowego. Określa on o ile przeciętnie wyniki danego funduszu różnią się od jego benchmarku/średniej porównawczej. Chcąc obliczyć wartość takiego miernika należy zastosować następujący wzór:


gdzie,
n-liczebność próby, y_i - różnica wyniku funduszu i benchmarku w momencie i,

Tak jak uprzednio, dla lepszej ilustracji problemu przedstawiamy obliczenia w tabelce. Do porównań wybrano Quercus Agresywny, dla którego benchmarkiem jest już wykorzystany wcześniej indeks WIG:

Ponownie, otrzymany wynik trudno oceniać w izolacji – otrzymane 1,89% należy interpretować na tle grupy. W istocie jest to wartość, która znajduje się niemal dokładnie w połowie stawki, więc trudno tu mówić o istotnie wyższym/niższym ryzyku zmienności na tle grupy.

Tracking error to wartościowa miara, ponieważ osadza ryzyko funduszu w pewnym kontekście – wiemy, jak przedstawia się zmienność w relacji do benchmarku czy średniej porównawczej. To pozwala nam szeregować rozwiązania według tej miary i lepiej ocenić ich zmienność, a czasem nawet stwierdzić czy faktycznie realizują deklarowaną politykę inwestycyjną. Zbyt wysokie tracking error może sugerować, że mandat zarządzającego jest wykorzystywany w odmienny od zakładanego sposób. Z drugiej strony, bardzo niski poziom wskaźnika może sugerować, że menadżer portfela stroni od ryzyka, nie oferując uczestnikom wartości dodanej.

W następnym odcinku cyklu skupimy się na wskaźnikach alfa i beta, opisujących selekcję oraz wrażliwość funduszu na zmianę średniej/benchmarku.

Marcin Różowski
Analizy Online

Reklama

Zapisz się na Newsletter

Bądźmy w kontakcie! Prosto na Twojego maila będziemy wysyłać skrót najważniejszych informacji ze świata finansów, powiadomienia o nowościach rynkowych, najnowsze oceny i raporty oraz codzienne notowania wybranych przez Ciebie funduszy inwestycyjnych.

Zapisz się